
My research is focused on the mathematical description of highly flexible systems with frictional contact.
Soft robotics and flexible multibody dynamics
- Dynamics and control of soft robots using finite element formulations
- Development of tailor-made simulation environments for flexible multibody systems
- Contact mechanics within the field of nonsmooth dynamics
Mechanical metamaterials and computational mechanics
- Development of novel mathematical theories for micro-structured materials
- Design, modeling and analysis of materials with second-gradient elasticity effects
- Variational formulations and numerical treatment of nonlinear beam theories

Recent publications
Second-gradient continua
Highlights
- Continua with deformation energies depending on first and second gradients of the placement map
- Synthesis of micro-structures with emerging second-gradient formulation on a macro scale
- Application of second-gradient theory to fiber reinforced composites
To date, there are essentially two different ways to postulate the foundations of classical continuum mechanics, which is also known as first gradient continuum mechanics. The first method, called Cauchy continuum mechanics, has been conceived mainly by Cauchy and assumes forces and moments of forces as the primitive concepts together with the formulation of corresponding balance laws, and, by means of the tetrahedron argument, on the introduction of the concept of stress. The second method, which traces back to D'Alembert, Lagrange, Piola and Hellinger, is of variational nature and uses virtual work functionals as primitive concept. Such a formulation of continuum mechanics is therefore called D'Alembert-Lagrange continuum mechanics and postulates as its fundamental law the principle of virtual work, which demands the total virtual work functional of a body to vanish for arbitrary admissible virtual displacements.
While the generalization of Cauchy's theory is almost impossible, following D'Alembert-Lagrange continuum mechanics, it is conceptually straightforward to generalize the classical first gradient theory to a second-gradient theory. In fact, second-gradient continua are such continua whose internal virtual work functional depend not only on the first \(\delta F^i_A\) but also on the second gradient \(\delta \mathbb{F}^i_{AB}\) of the virtual displacement \(\delta \Pi\) given in the form \[\delta W^\mathrm{int}(\delta \Pi) = -\int_{\Omega} (P_i^A \delta F^i_A + \mathbb{P}_i^{AB} \delta \mathbb{F}^i_{AB}) \mathrm{d}V \, ,\] where \(\Omega\) denotes the reference configuration and \(P_i^A\) and \(\mathbb{P}_i^{AB}\) are the components of the Piola-Lagrange stress \(P\) and the Piola-Lagrange double-stress \(\mathbb{P}\). The theoretical definition of such a continuum is much easier, than answering the following key question: "Is there a micro-structured material whose deformation behavior is described by a mathematical theory in which the second gradient of placement dominiates?"

This question could be answered by the development of materials with pantographic micro-structures, as for instance the bi-pantographic fabric metamaterial. In the lab, these materials or structures can be fabricated with a micro-structure on a centimeter scale. Nevertheless, we could show that already for a relatively low number of cells, a second-gradient continuum formulation is suitable to describe the macroscopic behavior of the material, i.e., when it is considered as a two-dimensional continuum. The continuous description was obtained by an asymptotic homogenization starting from a deformation energy of a discrete system.
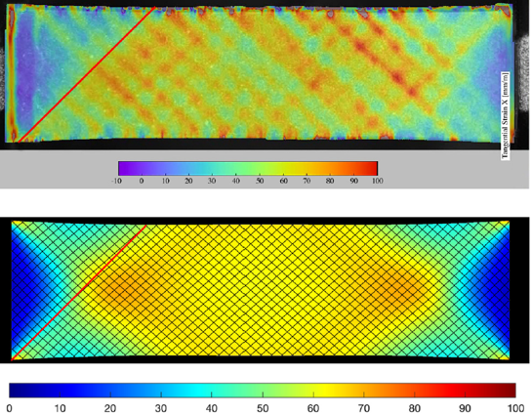
Equipped with the theoretical skills from second-gradient theories, we discovered second gradient behavior also in fiber reinforced composites. In fact, experiments advised us that the fibers' in-plane curvatures contribute significantly to the deformation energy and are required to find material parameters that are independent of the initial inclination angle of the fiber families.
The theory of second, and also higher gradient continua, brings many interesting research perspectives. For instance, on a theoretical level, the augmented internal virtual work functionals allow for non-standard boundary conditions, where not only surface forces do appear. These additional boundary conditions are studied by us on a mathematical level and will be evaluated in future also in experiments. Hence, we must face the challenge to design generalized clamping mechanisms for micro-structured continua to induce the theoretically obtained boundary conditions. Another challenge is the downscaling of the micro-structure to realize second-gradient material, where the micro-structure is not visible to the eye.
Publications
Nonlinear beam theories
Highlights
- Beam theories as intrinsic and induced theories
- Homegenization: from discrete structures to beams
- Finite element formulations that allow for large displacements and large strain
- Simulation frameworks for micro-structured continua and flexible multi-body systems
The terminology of beams and rods is widely used and a myriad of different understandings coexist. In our research, we consider beams as generalized one-dimensional continua that model the mechanical behavior of three-dimensional beam-like objects; often these are slender deformable bodies or structures. While a one-dimensional continuum corresponds to a deformable curve in space, parameterized by a single material coordinate and time, a generalized continuum is augmented by further kinematical quantities depending on the very same parameters.
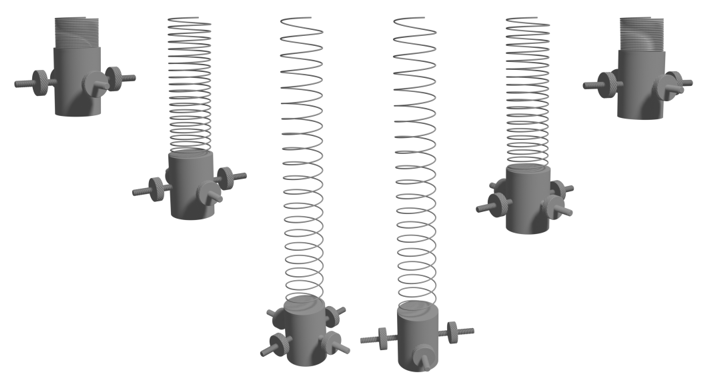
A fundamental challenge for beam theories is to find the governing equations to describe such a one-dimensional continuum. We are working on several procedures, all of which have in common to be based on the principle of virtual work. This means that also beam theories can be considered as a part of D'Alembert-Lagrange continuum mechanics. Beam equations can be obtained as intrinsic theories, in which objectivity arguments of the deformation energy lead to the relevant set of generalized strain measures and consequently to the internal virtual work functional of the beam. Sometimes it is also convenient to consider beams as induced theories, where a beam is understood as a constrained three-dimensional continuum. However, also homogenization methods can be used to translate a system of many discrete cells into a continuous formulation.

The formulation of beam theories within the variational framework of the principle of virtual work has also advantages in the development of numerical procedures to solve the governing equations. Indeed, the virtual work functionals are the direct entry to Galerkin methods. We are developing finite element formulations of planar and spatial nonlinear beam theories with a special interest in the following topics. To be capable of solving problems with high differentiability requirements, we are focusing on B-Spline interpolations. For large rotations, the element formulations must conserve the objectivity of the continuous theory. Moreover, singularity problems of rotation parameterizations are also studied. Satisfying the before mentioned requirements, our beam formulations are widely applicable and are used within meso-scale modeling of micro-structured continua as well as in flexible multi-body systems.
Beam theories also guide us as building blocks to develop models of two- or three-dimensional generalized continua. For instance, the second-gradient continuum formulation of a body with a lattice micro-structure has been obtained starting with the beam equations of the spatial Euler-Bernoulli beams. Similarly, the pantographic beam formulation was used to develop models for a planar second-gradient continua.
Publications
Nonsmooth mechanical systems
Highlights
- Generalized-alpha time integration scheme for mechanical systems with frictional contact
- Temporal finite element discretizations for the derivation of numerical time integration schemes
- Modeling and simulation of the inversion phenomenon of the tippedisk
In many engineering applications, systems are modeled through rigid and flexible bodies, which are interconnected by joints and can come into contact with each other or their surroundings. Prominent examples are automotive and robotic systems. The dynamics of mechanical systems with frictional contact can be described within the theory of nonsmooth mechanics, where the velocities of the system are allowed to jump. This is particularly important for the description of contact between rigid bodies, where at the time instant when the contacting bodies touch, an impact might occur, which due to rigidity instantaneously changes the velocity of the body.
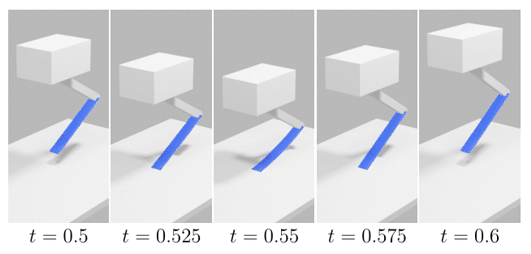
In our research, we are developing numerical time integration schemes for nonsmooth mechanical systems. Hence, the integrators must be able to handle unilateral constraints and set-valued friction laws. To evaluate and improve the obtained integrators, we are constantly investigating the dynamic behavior of systems in which collision and friction phenomena occur.
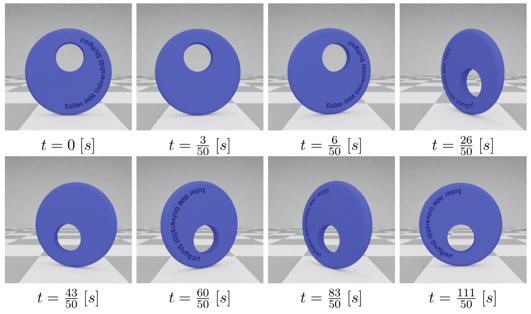
For instance the tippedisk, which is a spinning object consisting of a thin disk for which the center of mass does not coincide with its geometric center. When spun around an in-plane axis an interesting inversion phenomenon can be observed.
Publications
Links
Geometric mechanics
Highlights
- Differential geometric theory for time-dependent finite dimensional systems
- Lagrange's and Hamilton's equations of motion are mere coordinate representations of the same coordinate free postulate
- Interconnections between classical equations from analytical mechanics
The language of differential geometry allows a coordinate-free representation of physical quantities. This led to the development of several geometric theories for the description of finite-dimensional mechanical systems. These approaches differ in the mathematical concepts they invoke and in the classes of mechanical systems they can describe. For instance, when considering the motion of the mechanical system as a curve in the system's configuration manifold, only position dependent forces can be intrinsically formulated. When working in the framework of symplectic manifolds, i.e., when formulating the dynamics on tangent or cotangent bundles of the configuration manifold, forces can also depend on velocities enabling the treatment of dissipative systems. However, to include also explicitly time-dependent forces, the geometry must be adapted once again.
Using the non-standard geometric structure proposed by Ottmar Loos in a typescript
related to a seminar held in the winter semester 1981/1982 (O. Loos, Analytische Mechanik, 1982, scanned:
,
new typeset:
), we elaborated
a coordinate-free formulation of the theory for time-dependent finite-dimensional mechanical
systems with n degrees of freedom. The state space containing the system’s information on time, position and velocity is defined
as a (2n+1)-dimensional affine bundle over an (n+1)-dimensional generalized
space-time. We presented a geometric postulate that characterizes a second-order vector field whose integral
curves describe the motions of a
time-dependent finite-dimensional mechanical system. The core objects of the
postulate are differential two-forms on the state space, called action forms, which
are in a bijective relation with second-order vector fields. The requirements for
a differential two-form to be an action form allow for a coordinate-free definition
of non-potential forces, which may depend on time, position and velocity.
Within this theory, we elaborated the interconnections between
classical equations known from analytical mechanics such as the principle of
virtual work, Lagrange’s equations of the second kind, Hamilton’s equations,
Lagrange’s central equation, Hamel’s generalized central equation as well as
Hamilton’s principle.
Publications
Further Publications
Soft robotics
Highlights
- Tailor-made simulation environments for soft robotic systems
- Experimental set-up of a tendon-driven joint module to evaluate control and state estimation concepts
Nature's diversity has inspired scientists and engineers for centuries. The recent technological progress in material design and manufacturing processes has enabled a progressive transfer of nature’s conceptions to robotics and has led to the field of soft robotics. With a paradigm shift from rigid to soft, devices made out of highly deformable materials are developed in such a way that they intrinsically satisfy design criteria such as high flexibility, mechanical robustness, safe human-robot interaction, energy storage or shock absorbability. Soft robots are commonly actuated in two ways: by tendons with variable length routed along or within the body, or by pneumatic actuation which causes the system to deform by changing pressure level. Even though many soft robots have been tested, general modeling and control methods are still not available.

Taking insights from structural and continuum mechanics, we are working on modeling and simulation frameworks for a systematic design and control of soft robots. In collaboration with the Institute of Robotics and Mechatronics from the DLR, Oberpfaffenhofen, Germany, we are developing a soft material tendon-driven serial manipulator composed of stacked joint modules. Naturally, the development of the manipulator poses novel research questions concerning design, fabrication, modeling and control, whose answers will get us to a new generation of soft robots.
Publications
Funding and project partners
History of mechanics
Highlights
- Annotated translation of the fundamental review article "Die Allgemeinen Ansätze der Mechanik der Kontinua" by Ernst Hellinger.
- Continuum mechanics based on the principle of virtual work has always been coexisting besides Cauchy's version of continuum mechanics.
There are several motivations for us to spend time with historical texts in mechanics. The most important one is to learn from the maestros. The study of the origins of scientific theories educates us in understanding the creative process of formulating novel scientific theories. Moreover, it guides us to the most powerful and far-reaching theoretical tools that have been used. With the translation of historical texts into English, as a secondary motivation, we want to counteract the loss of knowledge in mechanics and to conserve the inheritage of the European scientific community that did not publish in English.
The application of variational principles in continuum mechanics is in the mainstream of mechanical science still highly controversial. Sometimes such principles are even rejected as being logically inconsistent and not physically well-grounded. However, many of such questions have already been answered in elder papers not written in English. A crystal-clear article on that topic is the fundamental review article of Ernst Hellinger “Die allgemeinen Ansätze der Mechanik der Kontinua”. Following his predecessors J.-L. Lagrange, G. Piola and the Cosserat brothers, Hellinger presents in this treatise a nonlinear field theory of continuum mechanics entirely based on a variational principle “the principle of virtual displacements”, today referred to as principle of virtual work.
The collection of forces and stresses of any kind [...] have in common, that for any virtual displacement they expend a virtual work

We published a side-by-side translation as well as an exegetic series which intends
- to allow all non German-speaking mechanicians, physicists and mathematicians the reading of a crystal-clear and still topical article whose content has some enlightening parts,
- to trace the origins of current ideas of mechanical sciences to their original sources,
- to show that only one century ago the principle of virtual work (or virtual displacements/velocities) was regarded as the central principle in continuum mechanics and that Hellinger did forecast already then the main lines of its development,
- to discuss some technical and conceptual aspects of the variational principles in continuum mechanics which some authors consider still controversial.
Side-by-side translation in Evaluation of scientific sources in mechanics
Exegetic Series appeared in ZAMM
Introduction and Section I
Section II and III.A
Section III.B
The paper by Eugster and dell’Isola introduces Hellinger’s work to the international readers. Undoubtedly, this paper is an important contribution since it points to significant and still relevant developments in mechanics, more than century old, which have not been widely available due to the language of the original work. Even more importantly, the current papers goes beyond mere translation and places into a wider context the fundamental nature of Hellinger’s work and how the field of mechanics has been poorer for lack of its ready availability. The style of the current paper makes it highly readable. The concepts are presented in a way accessible to more modern students of mechanics by relating Hellinger’s work to the newer concepts and notations. The authors’ unique style, their accompanying commentary, their critical interpretations and explanations, and the references to modern works, many of which inadvertently follow concepts formulated by Hellinger, makes the current paper novel and of interest from theoretical as well as practical viewpoints. The paper makes a powerful and persuasive case for the centrality of the “variational ansatz” to mechanics. In an era of over reliance on numerical approaches without proper attention to their foundations this paper is timely and well-written, and, therefore deserves prompt publication. Reviewer 1, Exegesis of Introduction and Sect. I
This is a history of mechanics of major importance and significance. Here the authors show the primary role played by Hellinger (and his intellectual predecessor, Piola) in formulating modern mechanics. The paper is well written and comprehensively documented. It is wonderful and engaging to read. By bringing Hellinger (and Piola before him) to the wider community, the authors do a great service. In particular, they establish beyond any doubt that contemporary ‘discoverers’ of important notions such as the ‘part-wise virtual-work principle’ are in fact merely re-discoverers of ideas already advanced by Hellinger (or Piola). In fact these revelations allow modern students to visit the original sources, and there to discover the original ideas stated clearly and without fanfare, in pleasant contrast to the modern rediscoveries. Beyond these virtues, the paper argues convincingly about the effect that changes in the ‘lingua franca’ can have on the evolution of science. If anything, the paper is too forgiving of the modern rediscoverers in failing to mention one very typical human failing: the need for recognition, however far one is from earning it. In my view the paper simply must be published! Reviewer 2, Exegesis of Introduction and Sect. I
The paper is a major contribution to the history of Mechanics and should be published. Like the first paper of this series, this one is a masterpiece of scholarship, one that rights many historical wrongs committed by successors in their zeal to make a mark on the subject. Reviewer 1, Exegesis of Sect. II and III.A
As the title suggests, the work contains not only the translation of Hellinger’s work, but also a historical perspective on his works and of the evolution of continuum mechanics in general. The reading is very interesting and surprising in terms of contents and style. The authors balance very well translation, comments and historical considerations. The manuscript is very well written and easy to read. I consider that this work deserves publication in the present form. Reviewer 2, Exegesis of Sect. II and III.A
This is the third in a series of papers by Eugster and dell’Isola that, through translation of the work by Hellinger and the accompanying commentary by the authors, will bring to a wider audience the significant and powerful developments in mechanics, more than century old, which have not been widely available due to a variety of reasons lucidly discussed by the authors. Indeed the authors utilize the translation as a vehicle to discuss the factors that often control the state of scientific progress while faithfully and carefully discussing/commenting and highlighting the centrality of “variational ansatz” in Hellinger’s approach to continuum field theory. The third paper of the trilogy by Eugster and Dell’isola then completes the arguments from both the scientific perspective and the view of socio-politics of scientific endeavors. The style and content is even more persuasive the third time. The overall ‘package’ conceived by the authors is novel, besides being timely in this era of proliferating publications each of which proclaims unique contributions while almost pathologically giving short shrift to the preceding contributions. The resulting trilogy will not only serve pedagogical purposes for students learning variational methods but also shed light on socio-political factors related to art of publication, progress in science and the role of dominant personalities, the ‘pioneers’ versus the ‘colonists’. This paper, therefore, as its preceding ones in the series, deserves prompt publication. The paper has been carefully edited and suffers from only a very few minor editorial issues. This paper can be accepted as is without revision. Reviewer 1, Exegesis of Sect. III.B
This is a salacious paper in which the authors maintain that a large part of the insights given in the studies Truesdell and W. Noll, “The non-linear field theories of mechanics” and Truesdell and R. Toupin, “The classical field theories” was actually available in a review article presented in 1913 by Ernst Hellinger. One of the Authors’ intent is to "prove...how derivative and unoriginal some recent and contemporary mechanicians truly are." In doing so, they provide a sarcastic description, and, to be honest, rather realistic, of what the milieu of contemporary mechanicians is like, arranged into rude gangs of Lagrangians/Hamiltonians and Truesdellians, always seeming to be balanced upon the razor edge between survival and self-destruction. [...] The fact is, I – sadly – agree with a couple of statements of the paper, that are: 1. the central role of variational methods for their heuristic potential, as shown by the history of science, and also by contemporary physics ("Lagrangians stay much more stably in the physics textbooks", i.e. molecular dynamics simulations); 2. the lack of independency of many contemporary young scholars, considering “gospel” the reference text of the clan they belong to, stimulated by our times of “fast and copious publication activity”.
As in the Shakespearian Montecchi vs. Capuleti saga, well described in Baz Luhrmann’s Romeo+Juliet as a conflict between gangs, everything ends up with the destruction of both sides, and of the dream of Love beyond borders, this paper probably epitomizes the decline of mechanics as a science in which it still makes sense to do Research. Reviewer 2, Exegesis of Sect. III.B
Further publications and links
Books
Journal publications
Book contributions
Proceedings
Doctoral thesis

Simon R. Eugster, Dr. sc. ETH
Associate Professor
Department of Mechanical Engineering
TU/e – Eindhoven University of Technology
Curriculum vitae
Since 2024, I am Associate Professor at the Eindhoven University of Technology in the Dynamics & Control section.
.
I studied mechanical engineering at ETH Zurich and received my BSc and MSc degrees in 2007 and 2009, respectively. For my PhD, I joined the Institute of Mechanical Systems, where I graduated under the supervision of Prof. Ch. Glocker in 2014. Thereafter, I moved to the newly founded Institute for Nonlinear Mechanics headed by Prof. R. I. Leine at the University of Stuttgart, where I got the position as Lecturer (Akademischer Rat). In 2018, I was Visiting Scholar in the group of Prof. D. Steigmann at the University of California, Berkeley, United States. In 2020, I became Senior Lecturer (Akademischer Oberrat) at the Institute for Nonlinear Mechanics (INM).
Teaching experience
|
Mechanics of nonlinear continua (SS15 – SS2023) Tensor algebra and analysis, nonlinear deformation, nonlinear strain measures, principle of virtual work, variational law of interaction, nonlinear material laws, local constraints. |
|
|
Dynamics of mechanical systems (WS15 – WS17, WS19 – WS23) Calculus of variations, principle of virtual work, Kane’s equations, Lagrange’s equations of motion, principle of Hamilton, holonomic and non-holonomic constraints. |
|
|
Technical Mechanics IV (SS19) Dynamics of gyroscopes, impacts of rigid bodies, wave equation, oscillations of continuous systems, approximation techniques for continuous systems, energy methods in elasto-statics |
|
|
Miscellaneous topics in mechanics (SS16 – SS18) Introduction to advanced mathematics for engineers such as real analysis and linear algebra for mathematicians, differential geometry, functional analysis. |
Supervision of doctoral students
Co-supervision of doctoral students
| 2020 – 2024 |
Maximilian Stilz – University of Freiburg, Freiburg, Germany Numerical analysis of mechanical meta-materials Main supervisor: Prof. S. Hiermaier, University of Freiburg, Freiburg, Germany |
| 2020 – 2022 |
Matteo Lai – University of Cagliari, Cagliari, Italy Computational methods for structural stability of thin axisymmetric shells Main supervisor: Prof. A. Cazzani, University of Cagliari, Cagliari, Italy |
| 2017 – 2019 |
Emilio Barchiesi – Università la Sapienza, Rome, Italy Synthesis of second gradient architectured meta-materials: Micro-to-macro approaches, numerical investigations, additive manufacturing and experimental validation Main supervisor: Prof. F. dell’Isola, Università la Sapienza, Rome, Italy |
| 2015 – 2019 |
Bastian Deutschmann – DLR, German Aerospace Center, Oberpfaffenhofen,
Germany Modeling and control for a class of tendon-driven continuum mechanisms Main supervisor: Dr. C. Ott, DLR, Oberpfaffenhofen, Germany |
Externally funded research projects
DFG project Soft material tendon-driven serial manipulators (granted)
DFG project Design, modeling and control of modular tendon-driven elastic continuum mechanisms
within Priority
Program 2100
Soft Material Robotic Systems
Organization of workshops and symposia
- Organizer of the minisimposium "Nonlinear mechanics of beam, plate and shell structures: models and methods" at the ICoNSoM 2022
, Alghero, Sardinia, Italy, 13–16 June 2022
- Local organizer of workshop of the GAMM Fachausschuss Dynamik und Regelungstheorie, Stuttgart, Germany, 31 March – 1 April 2022
- Section chair of Multi-body dynamics section at the 91st GAMM annual Meeting
2020@21
, Kassel, Germany, 15–19 March 2021
- Online Focus Meeting 2020 of DFG SPP2100 “Soft Material Robotic Systems”, 7–8 December 2020
- Workshop on Higher-Gradient Continua in cooperation with Prof. F. dell’Isola and the
International
Research Center M&MoCS
, held in Giuliano di Roma, Italy, 4–7 October 2017
Editorial and review activities
| since 2022 |
Editorial board member of Mathematics and Mechanics of Solids |
| since 2022 | Managing editor of Mathematics and Mechanics of Complex Systems |
I am regularly selected as a reviewer for the following international journals:
Journal of Elasticity /
ZAMM – Journal of Applied Mathematics and Mechanics
/
ZAMP – Zeitschrift für Angewandte Mathematik und Physik
/
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences
/
Journal of Computational and Nonlinear Dynamics
/
International Journal of Solids and Structures
/
Mathematics and Mechanics of Complex Systems
/
Mathematics and Mechanics of Solids
/
Continuum Mechanics and Thermodynamics
/
Mechanics Research Communications
/
Archive of Applied Mechanics
/
Applied Mathematical Modelling
/
Journal of Mechanics of Materials and Structures
/
Mathematics
Regular activity as reviewer for German Resarch Foundations (DFG) and the Alexander von Humboldt Foundation
- Address
-
Eindhoven University of Technology
Groene Loper 3
5612 AE Eindhoven
Netherlands - E-mail/Telephone
- Publication list
- The publication list was generated with the amazing BibTeX-js script
- External links
-
The links identified by this graphic point (
) refer to externally forwarded contents for which I do not claim any ownership. The responsibility lies with the respective external provider.
The external contents were reviewed when setting the link. It cannot be ruled out that the contents are subsequently changed by the respective providers. Should you be of the opinion that any of the external websites to which this page is linked infringe upon applicable law or otherwise have inappropriate contents, please notify me accordingly.


